Uno de los riesgos que señalamos repetidamente en nuestro trabajo “El Caballo del Diablo”, en cuanto a investigaciones previas a la nuestra, se refiere al hecho que una investigación debería servir para que un autor futuro pudiera retomar el trabajo de su homónimo predecesor, con la seguridad de continuar sus pesquisas con todas las garantías posibles de objetividad.
En la historia de Rennes, encontramos que ciertas partes del mito son transmitidas de boca en boca o de escritor en escritor con algunas nefastas consecuencias, la transferencia de diversas incorrecciones que no hacen sino perpetuar infundadas afirmaciones y ampliar un falso misterio. Podemos “comprender” que el mito se vea alterado por algunos intereses manifiestos. En el primer caso, cuando la leyenda es transmitida por el “boca a boca”, encontramos que siempre han existido personas muy interesadas en que Rennes continúe recibiendo la visita de miles de turistas que generan suculentos ingresos; en el segundo caso, cuando la información se transmite de un investigador hacia aquellos que retoman y continúan su legado, observamos que existen autores que han preferido “novelar” los hechos para otorgar a sus obras ese carácter, ese factor misterioso y emotivo que atrae al ser humano desde siempre, un factor que conocen y son capaces de manipular ciertos escritores para tratar de alcanzar el mayor número posible de ejemplares vendidos. Lo expuesto hasta el momento hace que nos veamos en la obligación de cuestionar prácticamente cualquier información, sea antigua o novedosa, referida a esta historia. Precisamente es cuando nos hallamos ante trabajos de investigación, cuando deberíamos poder ser capaces de otorgar un crédito suficiente a la veracidad de los hechos que son expuestos ya que, como apuntábamos antes, deberíamos poder continuar la investigación de forma segura sin ningún tipo de duda, o como mínimo con la duda razonable de ciertas incorrecciones “inevitables” causados por naturales errores humanos. Sin embargo y muy a nuestro pesar, tras estudiar un buen número de investigaciones nos encontramos que, en ocasiones, es necesario partir de cero y comprobar si los hechos que se nos muestran son veraces o no… Y esto se nos hace difícil de comprender…
Uno de esos falsos mitos sobre Rennes se refiere concretamente a la existencia de una supuesta simetría en el jardín de Villa Bethania. Se nos ha tratado de mostrar que esta zona ajardinada, situada entre la Torre Magdala en un extremo y el invernadero en su lado opuesto, formaría nada más y nada menos que un perfecto tablero de ajedrez, siendo la superficie de la torre el cuadrado base que delimitaría el área de un escaque. Si trasladamos esta superficie al terreno, obtendríamos un perfecto tablero de ajedrez de 8×8 casillas.
En la primera ocasión que conocimos y nos documentamos sobre esta teoría nos sorprendimos sobremanera. Para nosotros resultaba un hallazgo extraordinario, puesto que durante nuestro trabajo de campo, tal y como explicamos en el libro, nos proponíamos hallar indicios que nos sirvieran de base para tratar de argumentar que el creador del manuscrito largo, el emisor del mensaje cifrado, tal y como indica una de las principales normas de la criptografía, debería haber dejado al interceptor indicios que permitieran reseguir los pasos para el correcto descifrado del texto. Cuando vimos por primera vez la imagen que os presentamos a continuación, nos sorprendió percibirla en la posición que se nos mostraba:
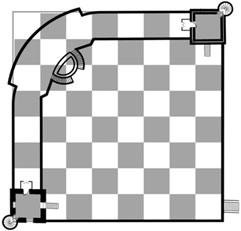
Generalmente la imagen suele mostrarse en esta posición en la mayoría de artículos, investigaciones y sitios web consultados, y esto nos pareció algo extraño, ya que carece de sentido mirar el tablero desde esta perspectiva en concreto. El acceso al jardín es desde Villa Bethania, por lo que lo más lógico, en una representación en plano, sería mirar la figura desde la posición de entrada. Observando la imagen con detenimiento, descubrimos algo muy interesante, algo que para nosotros podía resultar clave en nuestra busqueda de indicios. ¡La casilla 22 del tablero correspondia exactamente con la situación de las escaleras del jardín, escaleras que además están formadas por 22 peldaños! ¡Genial! ¡Bingo! ¡Ya lo tenemos! Esa fue nuestra reacción en ese momento, ya que creímos haber hallado una clara y contundente evidencia, evidencia que además podía comprobarse, sobre la casilla que inicia la secuencia de salto al aplicar el método de descifrado conocido como Salto del Caballo (F6=22).
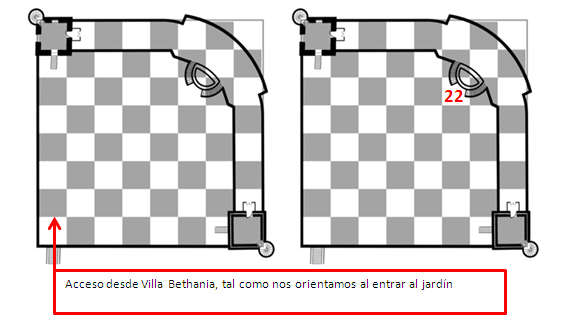
Evidentemente, para nosotros resultaba un hecho asombroso ya que, como apuntábamos anteriormente, resultaba algo esencial como indicio para la consecución de uno de los objetivos principales de nuestro libro, pensar como un interceptor del mensaje cifrado y buscar las pistas o indicios dejadas por el creador del código. Ahora sabíamos que “el jardín es un tablero de ajedrez y en el punto exacto que corresponde con el escaque 22, teníamos situada la doble escalera con 11 peldaños por lado (22 peldaños)”.
Estábamos ilusionados, parecía ser que nadie se había percatado de este hecho, ya que no hallamos referencia alguna en libros, documentos, o páginas de internet. Pero, pese a todo, debíamos ser fieles al objetivo que nos habíamos planteado desde el inicio de la investigación. Debíamos comprobarlo por nosotros mismos…
Nos pusimos manos a la obra para verificar si el hallazgo era cierto. Pensamos incluso en alquilar o adquirir un globo aerostático con una cámara incorporada y dejarlo volar sobre el jardín atado a un cable, para poder de esta forma realizar las fotografías aéreas oportunas. Otra posibilidad era la de utilizar un avión a control remoto, o tal vez una cometa donde adaptar la pequeña cámara. En este punto nos encontrábamos en situación de pensar cuál de estos métodos podía servirnos mejor y el coste que se derivaría de cada uno de ellos, para tratar de establecer un presupuesto. Pero en ese momento nos alcanzaron algunas dudas… ¿Deberíamos dar explicaciones en Rennes-le-Château? ¿Sería necesaria la tramitación de algún tipo de permiso? ¿Se nos permitiría hacerlo? Ante las dudas, descubrimos un por entonces “novedoso invento” que podría ahorrarnos dinero y realizar todas las comprobaciones sin necesidad de movernos de casa, pues por aquellas fechas, a principios del año 2005, Google hacía poco que había lanzado sus exitosos proyectos Google Maps y Google Earth. Esta herramienta podía permitirnos observar desde una vista aérea, tal y como pretendíamos, si la supuesta simetría podía comprobarse, además de la posibilidad de tomar medidas y calcular superficies de forma totalmente interactiva. Esto fue lo que observamos:

Si utilizamos la superficie de la Torre Magdala como área de un escaque base y la trasladamos sobre el área del jardín para tratar de formar un tablero de ajedrez de 8×8 casillas, el resultado es que no cuadra en absoluto, ni siquiera para formar un cuadrado. Para mayor seguridad, en este punto decidimos realizar algunos cálculos con la herramienta que lleva incorporada Google Earth. Cualquier investigador podrá comprobar por sí mismo los resultados obtenidos, que son los siguientes:
El área ocupada por la Torre Magdala es de 32,18 m2, con un perimetro de 22,71 metros lineales. Aunque estos cálculos, como podréis comprobar, son aproximados, también podréis observar que el desfase de medidas, comparando las medidas reales con aquellas que deberían resultar para formar una perfecta simetría con un tablero de ajedrez, es tanto que los pequeños fallos en que puedan incurrir las medidas tomadas por nosotros carecen apenas de toda importancia. Estamos hablando de centímetros, pero seamos estrictos y supongamos que fallamos por 2 metros:
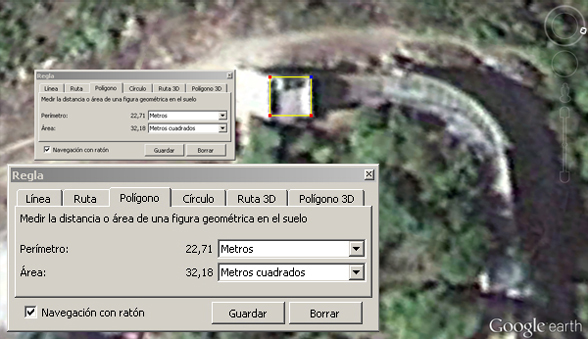
Si dividimos el perimetro entre los cuatro lados de la torre, obtenemos una longitud de 5,67 metros por cada uno. Si esto lo multiplicamos por 8, el número de escaques de un tablero de ajedrez, obtenemos un resultado de 45,42 metros totales para nuestro tablero imaginario, es decir, el lado del cuadrado debería ser de 45,42 metros. Esto nos da un perímetro total de 181,68 metros lineales y un área de 2059,52 m2.
Si ahora comprobamos las medidas de la superficie real del jardín con las herramientas de medición de Google Earth, obtenemos un perimetro de 134,56 metros. Eso significa que el lado real del cuadrado es de aproximadamente 33,64 metros. ¡Faltan unos 12 metros por lado para completar un cuadrado!
El área de la superfiie equivale a 1117,18 m2. Aún así, quisimos averiguar si el área total de la zona ajardinada podía corresponder con el total del área del cuadrado que buscabamos (2059,52 metros). ¿Quizás el área total del jardín equivalía al total de superficie del cuadrado, aunque su forma no fuese esta, sino más bien un rectángulo? Pero el resultado fue de nuevo decepcionante, ya que el área total del jardín corresponde a un total aproximado de 1511,22 metros. Todavía nos faltarían más de 500 metros cuadrados…
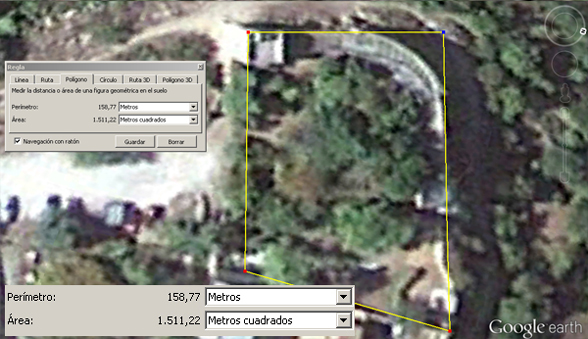
De todas formas, tampoco es necesario tomar medidas para observar, a simple vista, que no se trata de un cuadrado, sino que el área ajardinada presenta una forma rectangular.
En su momento, estas averiguaciones resultaron un auténtico mazazo para nuestra investigación, si recordamos lo enervados que nos encontrábamos cuando, al rotar la imagen y situar el tablero en la posición correcta, entrando desde Villa Bethania, las escaleras del jardín coincidían exactamente con el escaque 22. Pero este hecho demuestra, de nuevo si cabe, que una meticulosa comprobación de todo aquello que se ha dado por “bueno” en esta historia resulta absolutamente necesaria. Y es que de nuevo se viene afirmando un hecho que queda categóricamente descartado mediante un simple análisis. Aquello que para nosotros se aventuraba como un dificultoso día de investigación de campo, aviones teledirigidos, cometas voladoras, etc., se resumió en 4 horas de trabajo por ordenador. Las herramientas de análisis se encuentran accesibles, tan sólo se precisa la voluntad y el tiempo necesario para su empleo…
Alex Loro y Xavi Bonet





